3,80 von 5 Sterne
Loading...
Ausklammern und Ausmultiplizieren können am Anfang ganz schön verwirrend sein. Aber sobald du den Dreh raus hast, sind Klammern echt hilfreich. Hier lernst du alles, was du zum Thema Klammern wissen musst und kannst dies am Ende mit ein paar Übungen direkt verfestigen!
Du sollst einen Term faktorisieren bzw. ausklammern? Das bedeutet, dass du diesen zerlegen musst, indem du einen Faktor ausklammerst.
Faktorisieren in 3 einfachen Schritten
Wenn du einen Term durch Ausklammern faktorisieren möchtest, muss dieser zu Beginn eine Summe oder eine Differenz sein. Dies wird dann in ein Produkt umgewandelt.
- Eine Summe (Plus) stellt eine Addition dar.
- Die Differenz (Minus) bezeichnet eine Subtraktion.
- Ein Produkt (Mal) zeigt eine Multiplikation.
Bei dem ersten Beispiel wird der Term zunächst als Summe dargestellt. Sowohl die 5c, als auch die 5d enthalten die 5. Somit kann man sie ausklammern. Das Ergebnis ist dann ein Produkt mit der 5 außerhalb der Klammer und a und b in der Klammer.
Das zweite Beispiel zeigt eine Differenz. Deshalb steht in der Klammer jetzt ein Minus. Die 3 wurde hier ausgeklammert, weil beide Teil (3a und 3b) die 3 enthalten.
Man muss nicht unbedingt eine Zahl ausklammern, es kann auch eine Variabel oder eine Kombination aus Zahl und Variabel sein. Du musst nur darauf achten, dass alle Teile diesen Faktor auch enthalten.
Terme vereinfachen – wozu braucht man das?
Längere und kompliziertere Rechnungen können durch Umformen stark vereinfacht werden. Stell dir vor, du musst eine Äquivalenzgleichung nach x auflösen:
8 = 7xa +4xb – 3x
In jedem Einzelteil steht ein x, teilweise sogar mit anderen Variablen. Hier hilft dir das Ausklammern sofort:
8 = x (7a + 4b -3)
Schon steht das x alleine und du kannst durch den Term in der Klammer teilen:
\displaystyle \displaystyle\frac{8}{(7a+4b-3)}Deine Rechnung wird mit dem Vereinfachen, also wie das Wort schon sagt, vereinfacht und du kommst schneller zu deinem Ergebnis.
Ausmultiplizieren – wie rechnet man mit Klammern?
Beim Ausmultiplizieren hast du bereits Klammern in der Gleichung stehen und möchtest diese weg bekommen. Das Ausmultiplizieren ist im Grunde also der Gegenschritt zum Ausklammern.
Klammer auflösen – mit Beispielen zum leichteren Verständnis
Hier multiplizierst du den Faktor außerhalb der Klammer mit den einzelnen Teilen in der Klammer. Das heißt die 3 wird mit den 2a und dann mit den 5b multipliziert. Das kannst du dann im zweiten Schritt wie im Beispiel vereinfachen.
In diesem Beispiel hast du 2 Klammern. Deshalb musst du jeden Teil in der ersten Klammer mit jedem Teil in der zweiten Klammern multiplizieren. Die Farben zeigen dir die einzelnen Teile, die du multiplizieren musst.
Binomische Formeln
Binomische Formeln zeigen beispielsweise wie man ausmultipliziert. Da du aber nun gelernt hast, wie man selbst ausmultipliziert und ausklammert, sollten diese kein Problem mehr für dich sein.
Wann ist es eine Minusklammer?
Eine Minusklammer erkennst du daran, dass vor der Klammer ein Minus steht. Dieses Minus ist im Grunde eine -1. Du rechnest also alles in der Klammer mal -1.
Minusklammer in 5 Minuten verstehen und anwenden
Jetzt weißt du schon, dass du alle Teile in der Klammer mal -1 rechnen musst. Du kannst dann einfach alle Vorzeichen von den Zahlen und Variablen umdrehen. Ein positives Vorzeichen wird zu einem Minus und ein Minus wird zum Plus.
Hier musst du beachten, dass die 4 positiv ist, wenn dort kein Vorzeichen steht. Da die 6 auch positiv ist, musst du wenn du die Klammer auflöst vor beide Zahlen ein Minus schreiben. Die Regel kannst du bei Variablen genauso anwenden:
Beispiel 1: 8 – (x-5) = 8 – x +5
Beispiel 2: 16 – (-x-y) = 16 + x + y
Tipps und Tricks zum Ausklammern und Ausmultiplizieren
Wenn du dir unsicher bist, ob du richtig faktorisiert hast bleibt dir noch die Probe. Du multiplizierst dein Ergebnis also wieder aus und prüfst ob du dann den ursprünglichen Term bekommst.
Manchmal sieht man den Faktor den man ausklammern kann nicht direkt. Zum Beispiel stehen vor den Variablen unterschiedliche Zahlen, die aber alle durch eine bestimmte Zahl geteilt werden können. Dies könnte wie im Beispiel rechts die 3 sein.
Gleichungen mit Klammern – Aufgaben zum Üben
Nun kennst du alle Regeln und kannst sie direkt hier anwenden. Die Übungen helfen dir, dein Wissen zu verfestigen.
a) 6x+6y-6z
b) 3xy +4x² -5x
c) 8ab – 8ac +8a²
d) 5x +3xy
e) 2ab + 1a
a) 6x+6y-6z = 6(x+y-z)
b) 3xy +4x² -5x = x(3y + 4x -5)
c) 8ab – 8ac +8a² = 8a(b – c + a)
d) 5x +3xy = x(5 + 3y)
e) 2ab + 1a = a(2b + 1)
a) 3(x+5y)
b) 2x(x-3)
c) (x+3)(y-2)
d) (x-7x)y
e) 10 – (3x+14)
a) 3(x+5y) = 3x + 15y
b) 2x(x-3) = 2x² – 6x
c) (x+3)(y-2) = xy – 2x + 3y – 6
d) (x-7x)y = xy -7xy
⇔ -6xy
e) 10 – (3x+14) = 10 -3x -14
⇔ -4 -3x
Ausklammern und Ausmultiplizieren – FAQ
Wann muss man ausklammern?
Wenn du aus einer Summe oder einer Differenz ein Produkt machen möchtest, musst du ausklammern. Dadurch kannst du je nach Aufgabe besser umformen, bzw. besser nach einer Variabel auflösen.
Wann muss man ausmultplizieren?
Wenn du einen Term mit einer Klammer hast und die Klammer weg soll, musst du ausmultiplizieren.
Wie kann man ausklammern?
Um einen Faktor auszuklammern, müssen alle Einzelteile der Summe oder der Differenz, diesen Faktor enthalten.
Was ist der Unterschied zwischen ausklammern und ausmultiplizieren?
Beim Ausklammern entsteht eine Klammer, vor welcher dann der ausgeklammerte Faktor steht.
Beim Ausmultiplizieren verschwinden die Klammern und der Faktor wird mit allen Elementen multipliziert.
Ist faktorisieren ausklammern?
Ja, beim faktorisieren bzw. ausklammern entsteht aus einer Summe oder einer Differenz ein Produkt.
Was passiert wenn ein Minus vor der Klammer steht?
Dann werden alle Vorzeichen in der Klammer umgedreht.
Konnten wir dir beim Ausklammern und Faktorisieren helfen?
Schreib uns gerne in den Kommentaren, wie dir der Artikel gefallen hat und schau bei unseren anderen Artikeln vorbei, die dir das lernen in Mathe leichter machen. Hier findest du alles von der Symmetrie bis hin zum Arithmetischen Mittel! Und hier kommst du zu unseren Artikeln zum Berechnen eines Mittelwertes, sowie zum Bilden der Quersumme.
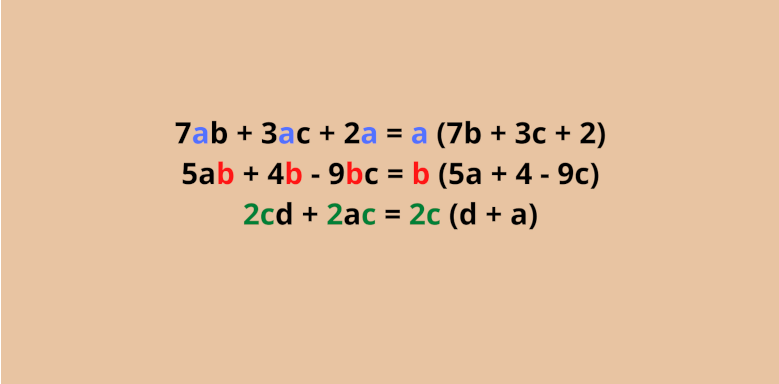
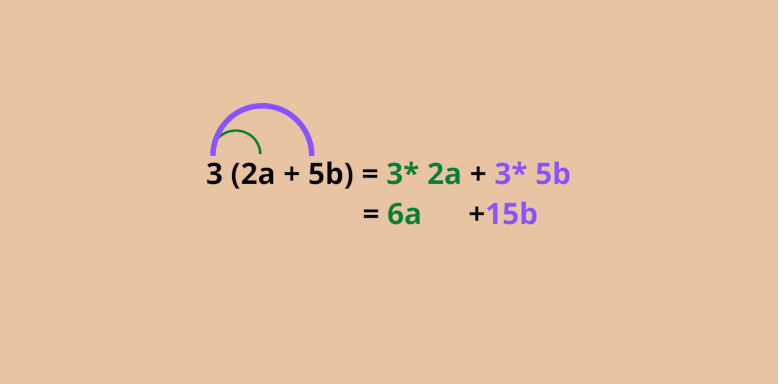
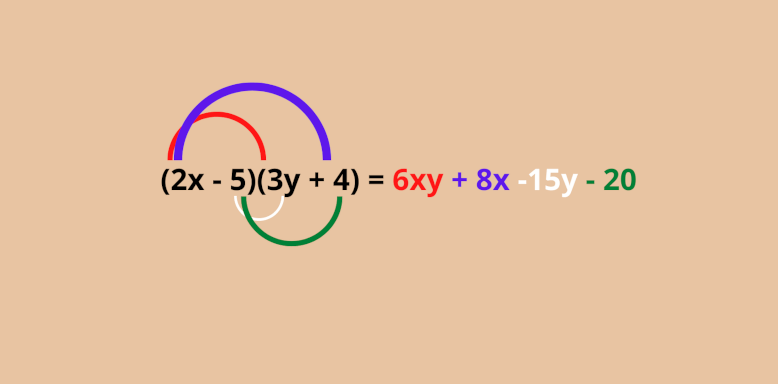
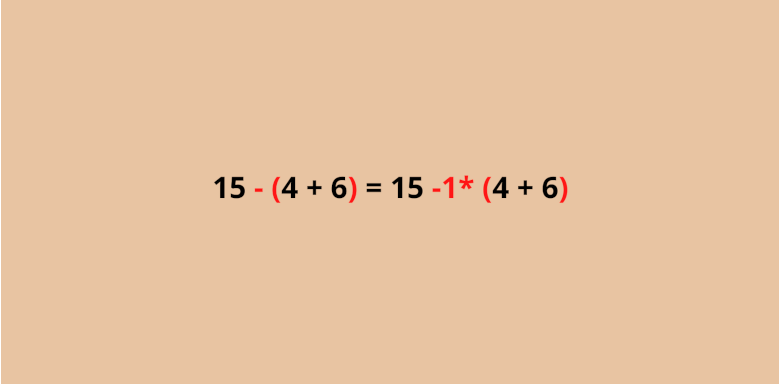
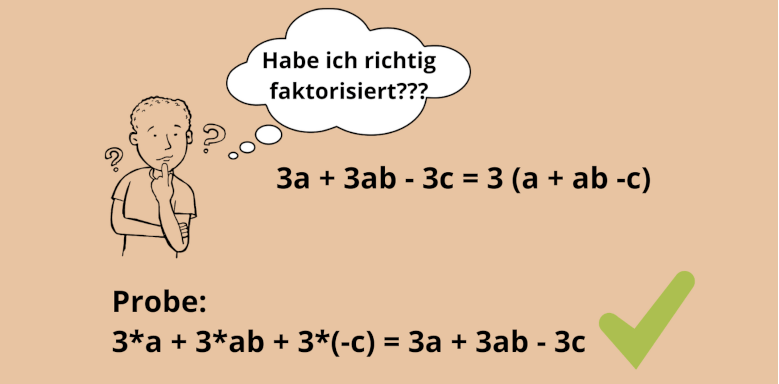
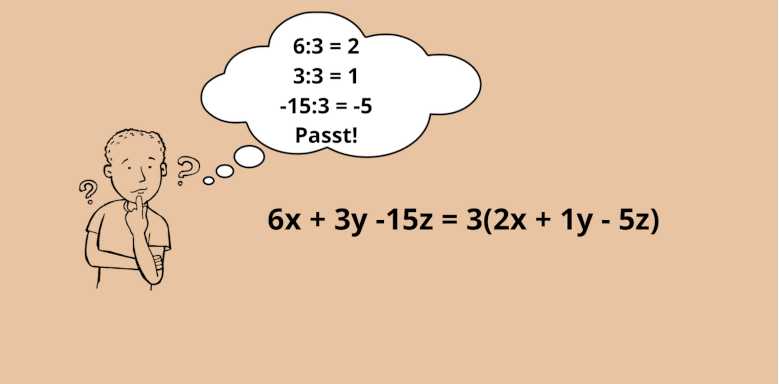
Vielen, vielen Dank. Ich bin begeistert. Es hilft uns allen sehr.?