4,33 von 5 Sterne
Loading...
Das Assoziativgesetz bereitet dir Kopfschmerzen und du möchtest es endlich verstehen? Kein Problem, wir helfen dir! In diesem Artikel lernst du alles, was du brauchst, damit du das Gesetz in Zukunft problemlos anwenden kannst.
Wie lautet das Assoziativgesetz?
(a+b)+c = a+(b+c)
(a•b)•c = a•(b•c)
Für was braucht man das Assoziativgesetz?
- Das Assoziativgesetz verwendest du bei reinen Multiplikationen und reinen Additionen, die Klammern enthalten.
- Also bei Rechnungen, bei denen entweder nur plus oder nur mal gerechnet wird.
Assoziativ – was heißt das überhaupt?
Das Wort Assoziativgesetz kommt vom lateinischen Wort associare. Das heißt “verbinden” oder “verknüpfen”. Deshalb wird das Assoziativgesetz auch Verknüpfungsgesetz genannt.
Fangen wir mit dieser Rechnung an:
Wenn du jetzt erst die Klammern auf beiden Seiten ausrechnest, erhältst du:
und diese Additionen ergeben:
Wie du siehst, sind beide Seiten von Anfang an gleich. Egal wo die Klammer steht.
Und das Gleiche noch beim Multiplizieren:
(7•6)•9 = 7•(6•9)
42•9 = 7•54
378 = 378
Auch hier
ist es egal,
wo die Klammern
sind
Das Assoziativgesetz gilt auch bei längeren Rechnungen mit mehr Klammern:
(1•(3•2•6)•(2•8))•9 = (1•3)•(2•6)•(2•8)•9
(1•36•16)•9 = 3•12•16•19
576•9 = 5184
5184 = 5184
3+((4+2+7)+(1+4)+(9+12)) = (3+4)+(2+7+1)+(4+9+12)
3+(13+5+21) = 7+10+25
3+39 = 42
42 = 42
Verknüpfen, vertauschen, verteilen – ein Überblick über die mathematischen Gesetze
Es gibt drei wichtige mathematische Gesetze, die du können solltest.
- Assoziativgesetze
- Kommutativgesetz
- Distributivgesetz.
Was ist das Kommutativgesetz?
- Das Kommutativgesetz besagt, dass du bei reinen Multiplikationen oder reinen Additionen die einzelnen Teile der Rechnung beliebig vertauschen kannst, ohne dass sich das Ergebnis ändert.
5+6 = 6+5
11 = 11
3•4 = 4•3
12 = 12
Was ist das Distributivgesetz?
4•(5+7) = 4•5 + 4•7
5•(9-3) = 5•9 – 5•3
- Beim Distributivgesetz geht es um das Ausmultiplizieren von Klammern. Dabei werden die Klammern entfernt.
- Um dies zu tun, multiplizierst du die Zahl neben der Klammern nacheinander mit den Zahlen in der Klammer.
Additionen verknüpfen
Wie wir oben gesehen haben, gilt das Assoziativgesetz für reine Additionen. Das sind Rechnungen bei denen nur + verwendet wird.
Schauen wir uns ein paar weitere Beispiele für das Assoziativgesetz bei Additionen an.
100+(513+12) = (100+513)+12
100+525 = 613+12
625 = 625
((85+90)+(17+34))+78 = 85+(90+17)+(34+78)
(175+51)+78 = 85+107+112
226+78 = 304
304 = 304
Assoziativgesetz bei der Multiplikation
Neben der reinen Addition kannst du das Assoziativgesetz auch bei der reinen Multiplikation anwenden. Auch hier bedeutet das “rein”, dass nur eine Rechenart verwendet wird. In diesem Fall das Malrechnen.
Hier nochmal zwei Beispiele:
30•(15•9) = (30•15)•9
30•135 = 450•9
4.050 = 4.050
5•((6•3•9)•8)•7 = (5•6)•3•(9•8•7)
5•((162)•8)•7 = 30•3•504
5•1.296•7 = 45.360
45.360 = 45.360
Hast du eine Rechnung, bei der plus und mal gerechnet wird, kannst du das Assoziativgesetz nicht anwenden. Es geht nur bei reinen Additionen und reinen Multiplikationen.
Beispiel:
2•(4+9) ≠ (2•4)+9
2•13 ≠ 8+9
26 ≠ 17
Subtrahieren und dividieren – hier kannst du nicht verknüpfen
Wir haben bisher immer nur von Additionen und Multiplikationen gesprochen und das hat auch einen Grund. Das Assoziativgesetz kannst du nicht anwenden, wenn minus oder geteilt gerechnet wird.
Wir zeigen dir auch warum.
Das passiert, wenn du die Klammer bei einer Subtraktion vertauschst:
(80-35)+40 ≠ 80-(34+40)
45+40 ≠ 80-74
85 ≠ 6
(10-6)-4 ≠ 10-(6-4)
4-4 ≠ 10-2
0 ≠ 8
Und hier siehst du, was das Verschieben der Klammer bei einer Division anrichtet:
(54:9)+9≠54:(9+9)
6+9≠54:18
17≠3
(100:10):2 ≠ 100:(10:2)
10:2≠100:5
5≠20
- Wie du siehst, sind hier die Ergebnisse auf beiden Seiten des “=” nicht gleich. Es macht also einen Unterschied, wo sich die Klammern befinden!
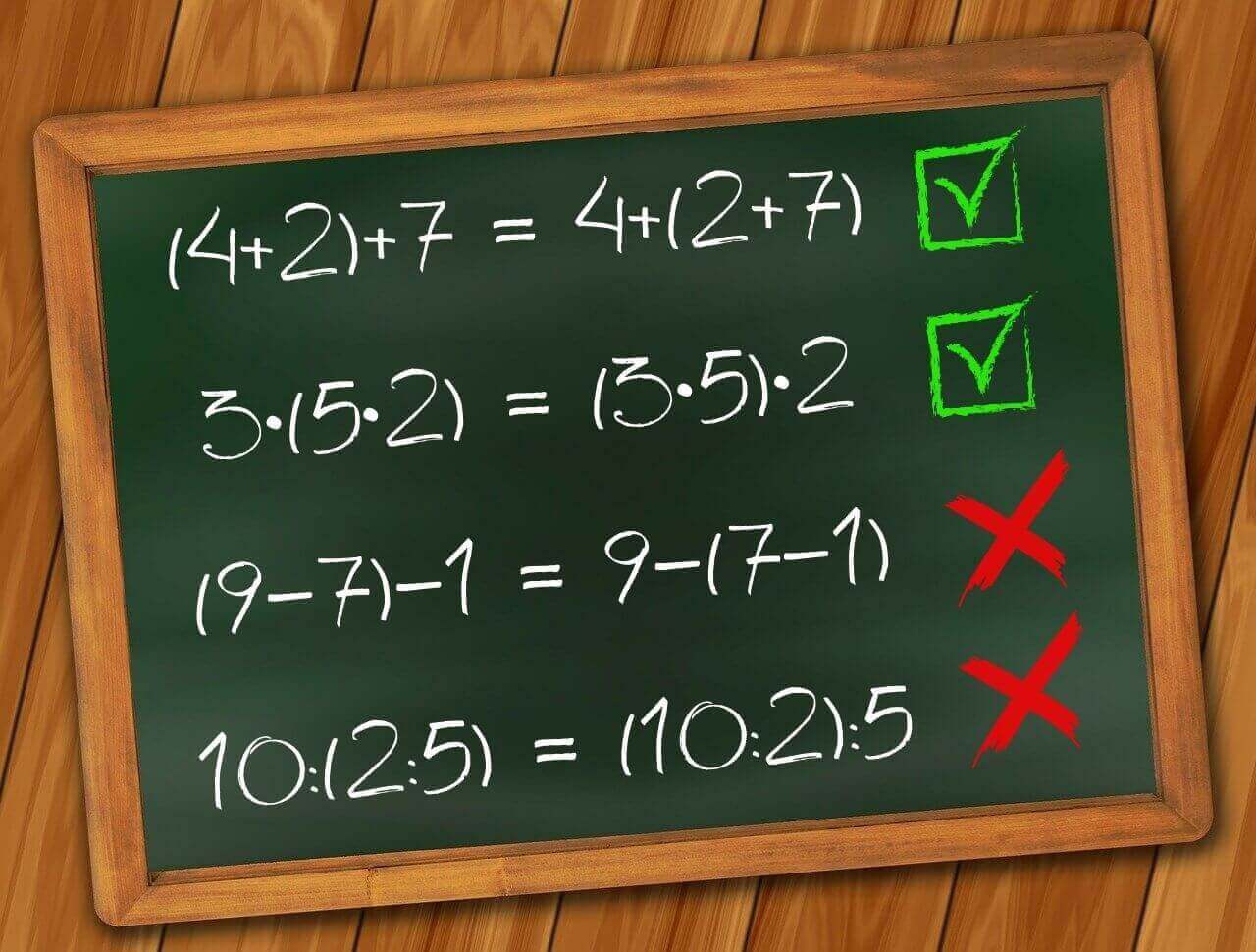
Assoziativgesetz – wann nicht verwenden?
Denk immer daran: Bei Subtraktionen und Divisionen kannst du die Klammer(n) nicht beliebig verschieben. Verknüpfen immer nur bei plus und mal.
Spickzettel
Hier kannst du unseren Spickzettel für dich runterladen.
Fazit:
Alle Fragen geklärt? Super! Wir freuen uns immer, wenn wir helfen können und wenn du magst, kannst du uns ein Kommentar dalassen.
Assoziativgesetz Übungen mit Lösungen
Wenn du willst, kannst du das Assoziativgesetz hier direkt ein bisschen üben:
Entscheide für jede Zeile, ob man das Assoziativgesetz anwenden und die Klammer(n) beliebig verschieben kann. Klicke einfach auf die Zeile, um die Lösung anzuzeigen.
Nein, da minus gerechnet wird.
Ja, da es eine reine Multiplikation ist.
Nein, da die Rechnung mehrere Rechenarten enthält.
Nein, weil dividiert wird.
Ja, weil es sich um eine reine Addition handelt.
Nein, weil die Rechnung verschiedene Rechenarten enthält.
Ja, weil es eine reine Multiplikation ist.
Du möchtest deine Mathe Kenntnisse noch weiter aufbessern? Dann schau doch gerne bei unserer Mathe Nachhilfe vorbei.
Egal ob bei dir Zuhause oder doch Online – das Nachhilfe-Team ist deutschlandweit tätig und steht den Nachhilfeschülern stets flexibel zur Seite.