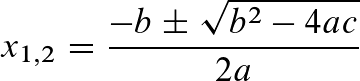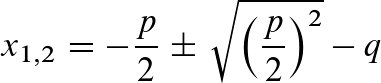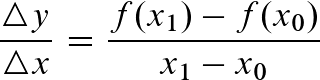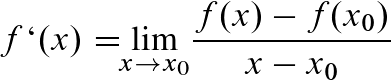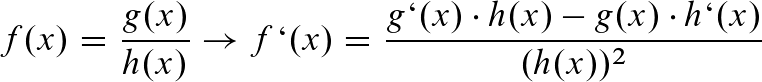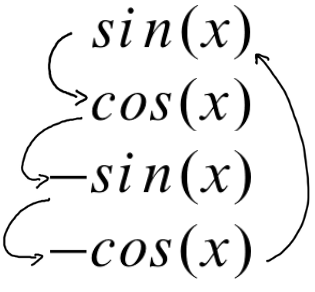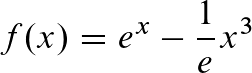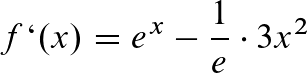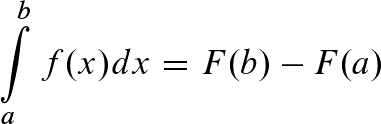5,00 von 5 Sterne
Loading...
Um einen guten Einstieg in das Thema Analysis zu bekommen und alles Andere zu meistern, zeigt dir dieser Artikel informativ, was zu den Grundlagen und weiteren Themengebieten der Analysis zählt.
Also legen wir gleich mal los!
Die Analysis bildet mit der Stochastik, Algebra und Geometrie ein Teilgebiet der Mathematik.
Grundlegend geht es bei der Analysis um Funktionen und das Herausfinden ihrer Eigenschaften und des Verhaltens.
Sie wird unterteilt in zwei Bereiche:
- Analysis 1, die sich mit Funktionen im eindimensionalen Bereich befasst und
- Analysis 2, die sich mit dem mehrdimensionalen Bereich auseinandersetzt.
Aber keine Sorge, in diesem Artikel geht es in erster Linie um Analysis 1. Wenn du schon bei Analysis 2 unterwegs bist, schau mal bei den Extremwertaufgaben vorbei!
Grundlagen der Analysis
Beginnen wir mal ganz gemütlich mit den Grundlagen. Sie werden dir auf jeden Fall bekannt vorkommen, weil Manches davon seit der 8. Klasse unterrichtet wird.
Klick dich einfach durch die einzelnen Punkte!
Ganz zu Beginn des Themas Analysis, werden die Zahlenmengen auf dich zu kommen. Hierbei geht es darum, dass du alle mal kennengelernt hast und weißt, welche Zahlen zu welcher Gruppe gehören.
Natürliche Zahlen
Die natürlichen Zahlen lernen wir schon von Beginn an kennen: sie beinhalten alle positiven Zahlen von 0 bis ∞.
0, 1, 2, 24
Reelle Zahlen
Reelle Zahlen beinhalten alle irrationalen und rationalen Zahlen.
Rationale Zahlen
Zu den rationalen Zahlen zählt alles, was du als Bruch, bestehend aus zwei ganzen Zahlen, schreiben kannst (auch Dezimalzahlen).
1 / 1,5 / ¼
Eine Potenz ist das Ergebnis des Potenzierens, wobei das Potenzieren eine abkürzende Schreibweise des Multiplizierens ist.
Nehmen wir mal folgendes Beispiel: 3*3*3 = 27. In Potenzschreibweise würde es so aussehen: 3³ = 27.
Wie bei allem anderen auch, gibt es hier bestimmte Gesetze, die befolgt werden müssen. Diese haben wir dir in unserem Artikel über Potenzgesetze ausführlich erklärt, also schau dort gerne mal vorbei!
Die binomischen Formeln sind dir sicherlich schon ein paar Mal über den Weg gelaufen. Natürlich dürfen wir die hier nicht vergessen.
Grundlegend sind diese Formeln dafür da, dir beim Ausmultiplizieren von Gleichungen die Arbeit zu erleichtern.
Falls du Hilfe bei binomischen Formeln hoch 3 (oder höheren Graden) gebrauchen könntest, dann schau mal bei unserem Artikel vorbei!
Die ABC-Formel (auch: Mitternachtsformel) und die pq-Formel werden zum Auflösen von quadratischen Gleichungen genutzt.
Wenn du die ABC-Formel benutzen willst, muss deine Gleichung folgende Form haben:
Die Formel hierfür lautet:
Themengebiete der Analysis
In diesem Abschnitt möchte ich dir die Themengebiete aus der Analysis einmal näher bringen. Sie sind unterteilt in:
- Funktionen
- Differentialrechnung
- Kurvenuntersuchung
- Integralrechnung
Funktionen
Starten wir mal bei den Funktionen. Wie am Anfang schonmal gesagt, bilden sie das Kernstück der Analysis, weshalb du das ganz genau lernen solltest.
Es gibt verschiedene Arten, die dir in der Analysis über den Weg laufen werden. Diese stelle ich dir hierunter einmal dar, mit Beispielen, wie sie aussehen könnten.
Eine Funktion ordnet jedem x-Wert genau einen y-Wert zu!
Klick einfach die Art der Funktion an, die du brauchst.
Ganzrationale Funktion / Polynomfunktion
Die Ganzrationale Funktion bildet die Summe von Potenzfunktionen und hat natürliche Exponenten.
Der Grad einer Polynomfunktion wird durch den Exponenten bestimmt, der als Erstes an der Reihe ist.
Unsere Funktion ist also vom Grad 3 und die Koeffizienten sind: 3, 6, -12, 24.
Quadratische Funktion
Eine quadratische Funktion erkennst du daran, dass sie ein Polynom vom Grad 2 hat.
Quadratische Funktionen haben die folgende Form, welche wir schon durch die Mitternachtsformel kennen:
Potenzfunktion
Was Potenzen sind, wurde schon im Abschnitt der Grundlagen mit abgeklappert. Jetzt sind die Potenzfunktionen an der Reihe. Die Form lautet:
Der Unterschied zu den Exponentialfunktionen ist, dass das x hier als Basis dient und nicht im Exponenten steht.
- a: reelle Zahl, ≠ 0
- n: gibt den Grad der Funktion an
- x: Basis
Exponentialfunktion
- b: Basis, > 0 und ≠ 1
- x: Exponent, reelle Zahlen
Natürliche Exponentialfunktion (e-Funktion)
Anstelle des b, kommt hier die Eulersche Zahl e als Basis hinzu.
Logarithmusfunktion
Die Logarithmusfunktion wird grundlegend als Umkehrfunktion einer Exponentialfunktion verstanden.
Sie hat folgende Form:
- x: Ergebnis
- b: Basis
- a: Numerus
x gibt an, mit welchem Exponenten die Basis b potenziert werden muss, um den Numerus a zu erhalten.
Natürlicher Logarithmus: ln (a)
- ist der Logarithmus zur Eulerschen Zahl e
- b = e
Winkelfunktion / Trigonometrische Funktion
Sie werden verwendet, um Zusammenhänge zwischen Winkeln und Seiten in einem rechtwinkligen Dreieck zu bestimmen.
Zu den trigonometrischen Funktionen gehören: Sinus, Cosinus und Tangens. Sie ordnet jedem Winkel, den y-Wert des Punktes P zu. Beispiel: sin (58,8º) = 0,9
Differentialrechnung
In diesem Themengebiet geht es jetzt darum, Veränderungen von Funktionen zu berechnen. Unter dem vorherigen Kapitel wurde gesagt, dass die Funktion jedem x-Wert genau einen y-Wert zuordnet. Jetzt geht es um Folgendes:
Sie befasst sich damit, wie stark sich der ausgegebene Wert ändert, wenn kleine Veränderungen an den Eingabewerten vorgenommen werden.
Ich hab noch zwei Begriffe für dich, die dir im Laufe des Themas über den Weg laufen werden. Schau sie dir einfach mal an, wenn du davon noch nichts gehört hast.
Es ist wichtig, dass du die beiden auseinanderhalten kannst und die Unterschiede weißt.
DifferenzENquotient
oder auch: durchschnittliche Änderungsrate, mittlere Änderungsrate
Gibt die durchschnittliche Änderung einer Größe in einem Intervall wieder.
Beispielsweise könnte eine Frage in der Klassenarbeit lauten:
Bestimme die Durchschnittsgeschwindigkeit des Autos für den Zeitraum xy.
Intervall [xo;x1]
DifferentIALquotient
oder auch: momentane Änderungsrate, lokale Änderungsrate, Ableitung
Gibt die momentane Änderung einer Größe zu einem bestimmten Zeitpunkt wieder.
Eine Frage in der Klassenarbeit könnte beispielsweise lauten:
berechne die Beschleunigung zum Zeitpunkt t0.
Stelle x0
Ableitungsregeln
Mittelpunkt der Differentialrechnung ist das Differenzieren oder auch Ableiten.
Die Ableitung entspricht hierbei, der Steigung der Tangente einer Funktion. Das wird in der Schule dann graphisch und rechnerisch geübt.
In diesem Abschnitt werde ich dir wichtige Ableitungsregeln zeigen, damit du einen groben Überblick gewinnen kannst.
Wenn du ausführliche Beschreibungen und Berechnungsbeispiele brauchst, schau bei unserem Artikel über Ableitungsregeln vorbei!
Hier unten kannst du dir die Regel anschauen, die du brauchst.
Potenzregel
Die Potenzregel zeigt dir, wie du eine Funktion mit Potenzen ableitest.
Summenregel
!Faktor a bleibt erhalten! Summandenweise ableiten!
Faktorregel
!Der Faktor a bleibt erhalten!
Quotientenregel
Die Quotientenregel wird benutzt, wenn du eine Funktion ableiten willst, die Brüche enthält.
Produktregel
Die Produktregel brauchst du für Funktionen, die aus einem Produkt bestehen.
Trigonometrische Funktionen
!Summand d fällt weg!
Das musst du dir unbedingt merken:
e-Funktion
Hier mal ein Beispiel, was ich meine:
Die Bestandteile mit dem e bleiben erhalten, diejenigen mit einem x werden auf normalem Weg abgeleitet.
!Achtung: ist e alleine als Summand angehängt, fällt es beim Ableiten weg!
Kurvenuntersuchung
Bei der Kurvendiskussion wird eine Funktion umfangreich untersucht, um wichtige Eigenschaften ermitteln zu können.
Ich werde dir hier die einzelnen Eigenschaften etwas genauer erklären, als Einstieg zum Thema.
Hier auch wieder: wenn du Schritt-für-Schritt Beispielberechnungen brauchst, schau bei unserem Artikel über Kurvendiskussion vorbei!
Integralrechnung
Die Integralrechnung befasst sich mit dem Berechnen von Flächeninhalten, die durch gekrümmte Linien begrenzt sind.
Ich werde dir hier wichtige Begriffe aufzeigen und ein wenig erklären.
Wenn du ausführliche Schritt-für-Schritt Beispiele brauchst, schau bei unserem Artikel über Integralrechnung vorbei!
Stammfunktion
Um nun die Fläche berechnen zu können, muss als erster Schritt die Stammfunktion gebildet werden (dieser Schritt wird integrieren genannt). Sie wird mit F(x) dargestellt und wenn wir diese differenzieren (also ableiten), erhalten wir die Funktion f(x).
Um die Stammfunktion zu bilden, machst du folgendes:
- Addiere +1 auf den Exponenten
- und multipliziere mit dem Kehrwert des neuen Exponenten
Hauptsatz der Integralrechnung
a = untere Grenze, b = obere Grenze / dx = Differenzial / f(x) = Integrant
Anwendung
- Bilde die Stammfunktion von f(x)
- Stammfunktion F(b): setze alle Werte der oberen Grenze für x ein
- Stammfunktion F(a): setze alle Werte der unteren Grenze für x ein
- F(b) – F(a)
- Ergebnis: Flächeninhalt A
Regeln der Integration
Genauso wie bei der Differentialrechnung und der Ableitung, gibt es auch hier bestimmte Regeln, die befolgt werden müssen. Ein paar wirst du deshalb schon kennen.
Zusammenfassung zum Thema Analysis
Die Analysis ist ein Teilgebiet der Mathematik und wird dich eine ganze Weile im Schulleben begleiten. In diesem Artikel will ich dir deshalb einen Überblick über die Themengebiete geben und was dich dort erwarten wird.
Zu den Grundlagen der Analysis gehören Zahlenmengen, die ABC- und pq-Formel, binomische Formeln, Potenzen und -gesetze.
Des Weiteren wird die Analysis in folgende Teilgebiete unterteilt: Funktionen im Allgemeinen, Differentialrechnung, Kurvenuntersuchung und Integralrechnung.
Lass uns noch eine Bewertung und/oder einen Kommentar da, wie und ob dir der Artikel weiter helfen konnte. Danke!
5,00 von 5 SterneLoading...
