Die Ableitung einer Funktion gehört zur allgemeinen Mathematik – du brauchst sie also immer wieder. Daher ist es wichtig, eine gute Übersicht über die verschiedenen Ableitungsregeln zu bekommen, auf die du dabei achten musst.
In diesem Artikel zeigen wir euch alle Ableitungsregeln und wann man sie anwendet.
Das heißt, ihr lernt:
- die Summenregel
- die Quotientenregel
- die Produktregel
- die Kettenregel
- die Potenzregel
- die Faktorregel
- wie man die e-Funktion ableitet
- besondere Ableitungen
Welche Ableitungsregeln gibt es?
Es gibt ganz einfache Funktionen, die du problemlos ableiten kannst.
Zum Beispiel bei f(x) = x+2 . Hier lautet die Ableitung einfach f'(x) = 1, da du nach x ableitest. Aber nicht immer hast du solche Funktionen gegeben, sondern es sieht schon etwas komplizierter aus. Dafür gibt es die Ableitungsregeln, die wir dir hier nun zeigen.
Zunächst eine kleine Tabelle zum Überblick für dich, welche Ableitungsregeln es alles gibt. Folgend gehen wir dann genausten auf jede einzelne ein.

Die Faktorregel
In den meisten Termen, für die du eine Ableitung berechnen wirst, kommen unbekannte Variablen in Form von x vor. Oft gibt es aber auch konstante Faktoren, die beim Ableiten erhalten bleiben.
Allgemein werden diese als c beschrieben ⇒ f(x) = c*g(x)
Beispiel:
f(x) = 4x
Abgeleitet bleibt die Konstante einfach bestehen. Hier wäre das dann f'(x) = 4
Die Potenzregel
Die Potenzregel zeigt dir, wie du die Ableitung einer Potenz bildest. Da die meisten Funktionen, die du ableiten wirst Potenzen sind, ist dies zu können grundlegend für dein Verständnis.
Im Allgemeinen sieht das so aus:
Du hast n als Exponenten, der bei x hochgestellt ist. Beim Ableiten nach der Potenzregel musst du nun den Exponenten als Faktor vor das x ziehen. Der Exponent vermindert sich um 1, daher steht im Exponenten jetzt n-1.
Die Summenregel
Die Summenregel ist die grundlegendste Ableitungsregel, mit der man die Ableitung einer Funktion finden kann, die aus der Summe von zwei Funktionen besteht. Hier leitest du beide Funktionen einzeln ab.
Die Funktionen lauten hier f(x) und g(x). So könnte deine Ableitung aussehen:
[(f(x) + g(x)]’ = f’(x) + g’(x)
Beispiel:
(5x² + 3x³)’ = (5x²)’ + (3x³)’ = 10x + 9x²
Ableitung Quotientenregel
Wie benutze ich die Quotientenregel?
Wenn du eine Funktion hast, die aus einem Bruch besteht, leitest du die Quotienten einzeln ab.
Die Formel hierzu lautet:
Die Ableitung des Zählers multipliziert mit dem Nenner minus der Ableitung des Nenners multipliziert mit dem Zähler, dividiert durch die Potenz des Nenners.
Du verstehst nur Bahnhof?

Z steht für den Zähler und N für den Nenner. Z’ ist der Zähler abgeleitet und N’ der Nenner abgeleitet. Mit dieser Formel kann man die Quotientenregel kurz darstellen.
Am Besten lernst du diese Formel auswendig:
Schritt für Schritt bedeutet das:
- Zuerst leitest du den Zähler ab und multiplizierst ihn mit dem Nenner:
g‘(x)*h(x) - Dann subtrahierst du den Zähler multipliziert mit der Ableitung des Nenners:
– g(x)*h‘(x) - Das Ganze teilst du dann durch den Nenner im Quadrat:
[h(x)]²
Ableitung Produktregel
Wenn du eine Funktion ableiten möchtest, die aus einem Produkt besteht, brauchst du die Produktregel.
So lautet diese allgemein:
f(x) = g(x)*h(x) ⇒ f(x)’ = g(x)’*h(x) + g(x)*h(x)’
Auch hier hilft leider nur auswendig lernen, oder du kannst dir diese vereinfachte Form merken:
U steht hier für Multiplikator 1 und V für Multiplikator 2. Da in einem Produkt die Reihenfolge keine Rolle spielt, sind diese auch austauschbar. U’ und V’ sind wieder jeweils die Ableitungen der einzelnen Funktionen.
Hier die Erklärung anhand eines Beispiels:
f(x) = (3+4x²)*(5x³+2)
Das kannst du dann noch vereinfachen:
f‘(x)=40x4 +16x+45x²+60x4
f‘(x)=100x4+45x²+16x
Ableitung Kettenregel
Wann brauchst du die Kettenregel? Wie der Name bereits verrät, benutzt du die Kettenregel bei einer Verkettung von Funktionen. Das bedeutet, eine Funktion ist mit einer anderen Funktion zusammengesetzt.
Das sieht dann so aus:
f(x) = g(h(x))
Erklärung anhand eines Beispiels:
2(3x+5)³
Hier hast du jetzt eine innere Funktion und eine äußere Funktion. Die innere Funktion ist 3x+5, die äußere Funktion ist 2()³. Diese beiden Funktionen musst du nun einzeln ableiten und danach nachdifferenzieren.
Was bedeutet das?
Wenn du die äußere Funktion nach der Potenzregel (siehe oben) ableitest, erhältst du 6()². Die innere Funktion in der Klammer bleibt vorerst stehen, also erhältst du: 6(3x+5)².
Nun musst du noch nachdifferenzieren, dass du die innere Funktion ableitest und mit dem restlichen Term multiplizierst.
Das Ergebnis deiner Ableitung lautet dann: 2(3x+5)³*3.
Spezielle Ableitungsregeln, die du kennen musst!
Es gibt besondere Funktionen, denen du immer wieder begegnest. Auch diese haben natürlich eine Ableitung und die meisten auch eine eigene spezielle Formel.
Ableitung Wurzel
Wurzeln begegnen dir nicht nur im Wald häufig, sondern auch in der Mathematik. Daher solltest du ihre Ableitung unbedingt auswendig können.

Ableitungsregeln sinus und cosinus
Auch diese besonderen Formeln haben eine spezielle Ableitung.
Die Ableitung des sinus ist der cosinus:
f(x) = sin(x) ⇒ f’(x) = cos(x)
Die Ableitung des cosinus ist der negative sinus:
f(x) = cos(x) ⇒ f’(x) = -sin(x)
Ableitungsregel tangens
Die Ableitung des tangens ist etwas schwieriger:
Ableitung e-Funktion und Logarithmus
Endlich wieder eine einfache Formel! Die e-Funktion wird gerade in den höheren Jahrgangsstufen viel verwendet. Ihre Ableitung ist eine dankbare Aufgabe, da sie unverändert bleibt.
Das heißt:
f(x) = e(x) ⇒ f’(x) = e(x)
Zuletzt gibt es noch die Logarithmusfunktion. Auch die hat eine Sonderableitung:
f(x) = ln(x) ⇒ f'(x) = 1÷x
Ableitungsregeln – 5 Übungen zum Nachrechnen
Das sind jetzt erstmal ziemlich viele Formeln. Hier hilft nur: Üben, üben, üben!
Daher gibt es hier noch ein paar Übungsaufgaben.
Leite folgende Funktion ab:
f(x) = 4x² + x³
Wende die Faktorregel und die Summenregel an:
f'(x) = 8x+3x²
Leite folgende Funktion ab:
f(x) = 4(x²+3x)³
Hier musst du die Kettenregel anwenden:
f'(x) = 12(x²+3x)² * 2x+3
Leite folgende Funktion ab:
f(x) = (x5-3) * (2x³+x²)
f‘(x) = (5x4)*(2x³+x²) + (x5-3x)*(6x²+2x)
Hier kannst du wieder vereinfachen:
f‘(x) = 10x7+5x6 + 6x7-18x³-2x6-6x²
f‘(x) = 16x7+3x6-18x³-6x²
Leite folgende Funktion ab:
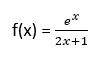
Hier musst du die Regel für die e-Funktion und die Quotientenregel anwenden:
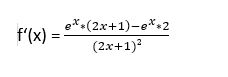
Leite folgende Funktion ab:
f(x) = cos(2x) * (3x-4)
Hier musst du die Regel für den cosinus und die Produktregel anwenden:
!Vorsicht! Denke an die Vorzeichen!
f'(x) = cos(2x)*3 – 2 sin(2x)*(3x-4)
Alles richtig gemacht? Dann solltest du jetzt alle Ableitungsregeln drauf haben!
Wenn nicht, einfach weiter üben.
Wenn dir dieser Beitrag geholfen hat, kannst du dir noch andere Beiträge von uns ansehen, die sich mit der allgemeinen Mathematik auseinandersetzen.

